സാമാന്യ ആപേക്ഷികതാസിദ്ധാന്തം
ഗുരുത്വം എന്ന പ്രതിഭാസത്തിനെ ജ്യാമിതീയമായി വിശദീകരിക്കുവാൻ ശ്രമിക്കുന്ന സിദ്ധാന്തമാണ്സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം (General theory of relativity). 1916 ൽ ആൽബർട്ട് ഐൻസ്റ്റീനാണ് ഇത് അവതരിപ്പിച്ചത്. അദ്ദേഹം തന്നെ മുൻപ് ആവിഷ്കരിച്ചിരുന്ന വിശിഷ്ട ആപേക്ഷികതാ സിദ്ധാന്തത്തിന്റെയും (Special relativity) സർ ഐസക് ന്യൂട്ടൺ ആവിഷ്കരിച്ചിരുന്ന സർവ്വഗുരുത്വാകർഷണനിയമത്തേയും ഏകോപിച്ച് ഉരുത്തിരിച്ച ഒരു സാമാന്യവത്കരണമാണ് ഈ സിദ്ധാന്തത്തിലൂടെ നിലവിൽ വന്നതു്. നിലവിലുള്ള ആധുനിക ഭൗതികശാസ്ത്രം ഗുരുത്വാകർഷണം എന്ന പ്രതിഭാസത്തെ അംഗീകരിച്ചിട്ടുള്ളത് ഐൻസ്റ്റീന്റെ സാമാന്യ ആപേക്ഷികതാസിദ്ധാന്തം അടിസ്ഥാനമാക്കിയാണ്.
ആൽബർട്ട് ഐൻസ്റ്റൈൻ മുന്നോട്ട് വച്ച വിശിഷ്ട ആപേക്ഷികതാസിദ്ധാന്തം, സാമാന്യ ആപേക്ഷികതാസിദ്ധാന്തം എന്നീ രണ്ട് സിദ്ധാന്തങ്ങളെ പൊതുവായാണ് ആപേക്ഷികതാസിദ്ധാന്തം എന്ന് വിളിക്കുന്നത് (Theory of relativity). ചുരുക്കരൂപത്തിൽ ആപേക്ഷികത എന്ന് മാത്രമായും പറയാറുണ്ട്.
വിശിഷ്ട ആപേക്ഷികതാസിദ്ധാന്തം (Special Relativity)
വിശിഷ്ട ആപേക്ഷികതാ സിദ്ധാന്തം രണ്ട് അടിസ്ഥാന പ്രമാണങ്ങൾ മുന്നോട്ടുവയ്കുന്നു.
- ചലനം ആപേക്ഷികമാണ്. ചലനത്തിന് ഒരു ആധാരം ഉണ്ട്.
- പ്രകാശത്തിന്റെ പ്രവേഗം സ്ഥിരവും കേവലവുമാണ്. പ്രകാശത്തിനാണ് ഏറ്റവും വേഗം.
ദൈർഘ്യത്തിന്റെ സങ്കോചം (Length contraction)
സമയ ദീർഘീകരണം (Time dilation)
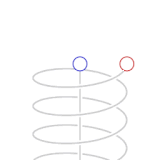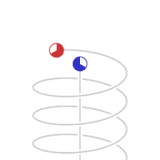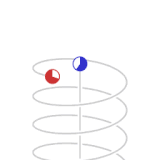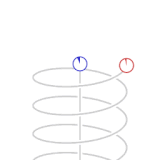 |
| From the local frame of reference (the blue clock), the relatively accelerated red clock moves slower |
ആപേക്ഷികതാ സിദ്ധാന്തത്തിന്റെ വിപ്ലവകരമായ മറ്റൊരു കണ്ടെത്തലായിരുന്നു സമയം ആപേക്ഷികമാണെന്നുള്ളത്. ഇതു പ്രകാരം നാമോരോരുത്തർക്കും വ്യത്യസ്ത സമയമാണ് ഉള്ളത്. അതായത് പ്രകാശവേഗത്തിൽ പോകുന്നയാളുടെ സമയം നിശ്ചലമായി നിൽക്കുന്ന ആളേക്കാൾ പതുക്കയേനീങ്ങൂ. ഇതുമായി ബന്ധപ്പെട്ട് രസകരമായൊരു ഉദാഹരണമുണ്ട്, ഇരട്ടകളുടെ വൈരുദ്ധ്യം.
ഇരട്ടകളുടെ വൈരുദ്ധ്യം (Twin paradox)
 |
| Minkowski diagram of the twin paradox. There is a difference between the trajectories of the two twins: the trajectory of the ship is equally divided between two different inertial frames, while the Earth-based twin stays in the same inertial frame. |
ദ്രവ്യമാന വ്യത്യാസം (Relativistic mass)
ദ്രവ്യോർജ അദ്വൈതം (Mass–energy equivalence)
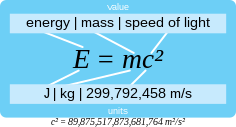 |
E = mc2 explained.
|
E=mc^2 എന്ന പ്രസിദ്ധമായ സമവാക്യം രൂപം കൊണ്ടത് ആപേക്ഷികതാ സിദ്ധാന്തത്തിൽ നിന്നുമാണ്. ദ്രവ്യവും ഊർജവും ഒന്നുതന്നെയാണെന്ന് ഐൻസ്റ്റൈൻ ഇതിലൂടെ സ്ഥാപിച്ചെടുത്തു. ദ്രവ്യവും ഊർജവും രണ്ടാണെന്നാണ് വളരെക്കാലം മുൻപുമുതൽ മനുഷ്യൻ പരിഗണിച്ചിരുന്നത്. ദ്രവ്യം ഊർജം എന്നിവ തമ്മിൽ പരസ്പരം മാറ്റാവുന്നതാണെന്ന കേവലസത്യം കണ്ടുപിടിച്ചത് മഹാഭൗതികജ്ഞനായ ഐൻസ്റ്റൈൻ ആയിരുന്നു. ഈ മഹാസത്യത്തെ ഗണിതപരമായി പ്രതിനിധീകരിക്കുന്ന സമവാക്യമാണ്
E=mc^2 ഇവിടെ E എന്നത് ഊർജ്ജം.
m എന്നത് ദ്രവ്യമാനം. c പ്രകാശത്തിന്റെ ശൂന്യതയിലുള്ള പ്രവേഗം. ശൂന്യതയിലെ പ്രകാശപ്രവേഗം ഔരു വിശ്വൈകസ്ഥിരാങ്കമാണ്.
velocity of light is 3*10^8 m/sec It means that light is the fastest moving thing in the world.
ഭൗതികവും ദർശനവും
ഐൻസ്റ്റൈന്റെ ദ്രവ്യ-ഊർജസമവാക്യത്തിന് ഭൗതികശാസ്ത്രത്തിൽ മാത്രമല്ല സാംഗത്യമുള്ളത്. നമ്മുടെ ചിന്താമണ്ഡലമാകെ കീഴ്മേൽമറിക്കുവാൻപോന്ന ഒരു പരമസത്യത്തിലേക്കാണ് അത് നമ്മെ നയിക്കുന്നത്. രണ്ടു വ്യതിരിക്തങ്ങളായ ഉണ്മകളല്ല ദ്രവ്യവും ഊർജവും, മറിച്ച് ഏകമായ പരമസത്യത്തിന്റെ ദ്വൈതാവതരണം മാത്രമാണ് അവ എന്ന് ഈ സമവാക്യം നമ്മെ ഉത്ബോധിപ്പിക്കുന്നു.
ആപേക്ഷികതയെപ്പറ്റി ഐൻസ്റ്റൈൻ തന്നെ പറഞ്ഞ ഒരു വാചകമുണ്ട് :
“ ഒരു സുന്ദരിയുമായി സംസാരിച്ചിരിക്കുമ്പോൾ കടന്നു പോയ ഒരു മണിക്കൂർ ഒരു സെക്കന്റായേ തോന്നൂ. എന്നാൽ കത്തി ജ്വലിക്കുന്ന വിറകിനടുത്ത് ഒരു സെക്കന്റ് ഒരു മണിക്കൂറായി തോന്നും ഇതാണ് ആപേക്ഷികത ”
What Is Time?
മുകളിലുള്ളതെല്ലാം നോകിയാല് നമുക്ക് മനസ്സിലാകാന് സാധിക്കുന്നത് സമയം ആപേക്ഷികമാണ് എന്നാണ് . ഇരുപതാംനൂറ്റാണ്ടിന്റെ തുടക്കത്തില് കേവലമായ കാലം, കേവലമായ സ്പേസ് എന്നൊന്നില്ലെന്ന് ആല്ബര്ട്ട് സമര്ത്ഥിച്ചു. എന്താണ് ആപേക്ഷികമായ സമയം? നമുക്ക് പരിശോധിക്കാം.
Solar Time
നമുക്കേറ്റവും പരിചയമുള്ളതും മനുഷ്യൻ ഏറ്റവും ആദ്യമായി മനസിലാക്കിയതും ആയ സമയത്തിന്റെ മാത്ര 'ദിവസം' ആണ്. ഭൂമിയിൽ സ്പേസിൽ ഒരു തവണ കറങ്ങിത്തീരുമ്പോൾ ഒരു ദിവസം കഴിഞ്ഞു എന്നു പറയുന്നു. ഒരു തവണ കറങ്ങി എന്നു നാം അറിയുന്നത് സാധാരണയായി സൂര്യനെ നോക്കിയാണ്. സൂര്യോദയം മുതൽ സൂര്യോദയം വരെയുള്ള ഈ സമയത്തെ 'സൗരദിനം' എന്ന് വിളിക്കുന്നു. ഭൂമി ആകെത്തന്നെ സൂര്യനുചുറ്റും സഞ്ചരിക്കുന്നതിനാൽ യഥാർഥത്തിൽ സൂര്യോദയം കഴിഞ്ഞ് സ്പേസിൽ പൂർണമായി ഒരു തവണ കറങ്ങുന്നതിന് മുമ്പുതന്നെ അടുത്ത സൂര്യോദയം ഉണ്ടാകുന്നതാണ്. ദൂരെയുള്ള ഏതെങ്കിലും ഒരു നക്ഷത്രത്തെ നോക്കിയാണ് ഭൂമിയുടെ കറക്കം നിർണയിക്കുന്നതെങ്കിൽ കൂടുതൽ ശരിയായ ദിവസം കിട്ടും. ഇതിന് 'നാക്ഷത്രദിനം' എന്നു പറയുന്നു. നാക്ഷത്രദിനം സൗരദിനത്തെക്കാൾ 4 മിനിറ്റ് നീണ്ടതാണ്. സാധാരണ ആവശ്യങ്ങൾക് നാം ഈ വ്യത്യാസം കണക്കിലെടുക്കാറില്ല. ഒരു ദിവസത്തെ 24 ആയി ഭാഗിച്ചാൽ മണിക്കൂറും അതിന്റെ 60 ആയി ഭാഗിച്ചാൽ മിനിറ്റും അതിനെ 60 ആയി ഭാഗിച്ചാൽ സെക്കന്റും കിട്ടുമെന്ന് നമുക്കറിയാം. അതുപോലെ ഭൂമി സൂര്യനുചുറ്റും ഒരു തവണ സഞ്ചരിക്കുമ്പോൾ ഒരു കൊല്ലം കഴിഞ്ഞുവെന്ന് നാം പറയുന്നു. അതിന്റെ 12 ൽ ഒന്നാണ് മാസം. അങ്ങനെ നമുക്ക് പരിചയമുള്ള എല്ലാ സമയമാത്രകളുടെയും അടിസ്ഥാനം ഭൂമിയുടെ ചലനമാണ്.
Pendulum
Animation of a pendulum showing the velocity and acceleration vectors.
തൂക്കിയിട്ട പെൻഡുലത്തിന്റെയോ വാച്ചിന്റെ ബാലൻസ് ചക്രത്തിന്റെയോ ആട്ടത്തെ അടിസ്ഥാനമാക്കിയും സമയത്തെ കുറിക്കാവുന്നതാണ്. ഞാത്തിയിട്ടിരിക്കുന്ന ഒരു പെൻഡുലം, അതിന്റെ ഒരു ആട്ടത്തിനുവേണ്ട സമയം ഒരു 'സെക്കന്റ്', ഇത് നമ്മുടെ ഇപ്പോഴത്തെ സെക്കന്റ് ആയിക്കൊള്ളണമെന്നില്ല. 100 സെക്കന്റ് 1 'മിനിറ്റ്', 100 'മിനിറ്റ്' 1 മണിക്കൂർ, നൂറു മണിക്കൂർ 1 'ദിവസം',100 ദിവസം 1'വർഷം'....ഇങ്ങനെ വേണമെങ്കിൽ സമയത്തെ നിർവചിക്കാം. അതനുസരിച്ച് ദിനചര്യകൾ ക്രമപ്പെടുത്തുകയും ചെയ്യാം. ഇവിടെ സമയത്തിന്റെ അടിസ്ഥാനം പെൻഡുലത്തിന്റെ ആട്ടമാണ്.
Atomic Clock
 |
| FOCS 1, a continuous cold caesium fountain atomic clock in Switzerland, started operating in 2004 at an uncertainty of one second in 30 million years. |
ആധുനികശാസ്ത്രലോകം സമയത്തിന്റെ ഏറ്റവും നിഷ്കൃഷ്ടമായ മാത്രയായി സ്വീകരിച്ചിട്ടുള്ളത് മറ്റൊന്ന്, എല്ലാ വസ്തുക്കളിലേയും തൻമാത്രകളും അണുക്കളും സദാ കമ്പിച്ചുകൊണ്ടിരിക്കുകയാണെന്ന് നേരത്തെ പറയുകയുണ്ടായല്ലോ. ഒരു നിശ്ചിത താപനിലയിൽ സീസിയത്തിന്റെ അണുക്കൾക്ക് 9 19 26 31 77 6 (ഉദ്ദേശം 920 കോടി) തവണ കമ്പിക്കുവാൻവേണ്ട സമയത്തെ ഒരു സെക്കന്റ് എന്ന് നിർവചിച്ചിരിക്കുന്നു. ഇപ്രകാരം വികൃതമായ ഒരു സംഖ്യകൊടുത്തിരിക്കുന്നത് ഇന്ന് പരിചയമുള്ള നക്ഷത്രസെക്കന്റിന് തുല്യമാക്കാനാണ്. ഭൂഗർഭവാസം അനുഷ്ടിക്കേണ്ടിവരുന്ന മനുഷ്യർക്, 1000 കോടി കമ്പനങ്ങൾക്ക് വേണ്ടിവരുന്ന സമയം ഒരു സെക്കന്റ് എന്നെടുത്താലും വിരോധമില്ല. ഇവിടെ സമയനിർവചനത്തിന് അടിസ്ഥാനമായിട്ടുള്ളത് അണുവിന്റെ കമ്പനമാണ്.
വേറേ വിധങ്ങളിലും സമയത്തെ നിർണയിക്കാവുന്നതാണ്. ഉദാഹരണത്തിന്, ദൃശ്യപ്രകാശത്തിനോ മറ്റേതെങ്കിലും തരത്തിലുള്ള വിദുത്കാന്തതരംഗത്തിനോ 3 ലക്ഷം കിലോമീറ്റർ സഞ്ചരിക്കുവാൻ വേണ്ട സമയത്തിനെ ഒരു സെക്കന്റ് എന്ന് നിർവചിക്കാം. രണ്ട് സ്ഥലങ്ങൾ തമ്മിലുള്ള ദൂരം അളന്നശേഷം, ഒരു സ്ഥലത്തുനിന്ന് പ്രകാശതരംഗങ്ങൾ അയച്ച് മറ്റേ സ്ഥലത്തുനിന്ന് പ്രതിഫലിപ്പിച്ച് തിരിച്ചെത്താൻ വേണ്ട സമയം എളുപ്പം നിർണയിക്കാം. ഇവിടെ പ്രകാശത്തിന്റെ ചലനമാണ് സമയനിർവചനത്തിന് അടിസ്ഥാനം.
Time dilation and Time travel
അങ്ങനെ ഭൂമിയുടെ കറക്കംകൊണ്ട് സമയം നിർവചിക്കാം. പെൻഡുലത്തിന്റെ ആട്ടംകൊണ്ടും സമയം നിർവചിക്കാം. അണുക്കളുടെ കമ്പനംകൊണ്ടും സമയം നിർവചിക്കാം. പ്രാകാശത്തിന്റെ ചലനംകൊണ്ടും സമയം നിർവചിക്കാം. നമുക്കറിയാം ആപേക്ഷികതാ സിദ്ധാന്തപ്രകാരം സമയം എന്നത് ആപേക്ഷികമാണ്. സമയം ഗുരുത്വാകര്ഷണ (gravity) ത്തേയും ത്വരണ(acceleration)ത്തേയും ആശ്രയിച്ച് വ്യതിചലിക്കുന്നുണ്ട്. ആപേക്ഷികതാസിദ്ധാന്തപ്രകാരം ശക്തമായ ഗുരുത്വാകര്ഷണ മേഖലയിലോ വര്ദ്ധിച്ച പ്രവേഗത്തിലോ സഞ്ചരിക്കുന്ന ഒരു വസ്തുവിന് സമയം പതുക്കെയാണ് അനുഭവപ്പെടുക. അതായത് പ്രകാശപ്രവേഗത്തോട് അടുക്കുന്തോറും സമയത്തിന്റെ ഇടവേളകള് ദീര്ഘിക്കുന്നു. ആറ്റോമിക് ക്ലോക്കുകളോ പെന്ഡുലമോ പഴയ മണല് ഘടികാരമോ എന്തുതന്നെ ആയിക്കൊള്ളട്ടെ, അവ ഒരേ പ്രവേഗത്തോടെയാണ് സഞ്ചരിക്കുന്നതെങ്കില് അവയ്ക്കുണ്ടാകുന്ന മന്ദതയും ഒരേ അളവിലായിരിക്കും. അതുപോലെ ശക്തമായ ഗുരുത്വാകര്ഷണ മേഖലയില് അകപ്പെട്ടിരിക്കുന്ന ഒരു വസ്തുവിനും സമയം മന്ദീഭവിക്കുന്നു. അതായതു ഗുരുത്വാകര്ഷകണബലം (gravitational force) കുറവായ/ഇല്ലാത്ത സ്പേസിലെ ഒരു ക്ലോക്ക് ചലിക്കുന്നതിലും പതുക്കെയാണ് ഗുരുത്വാകര്ഷഅണബലം ശക്തമായ ഒരു ഗ്രഹത്തിലെ ക്ലോക്ക് ചലിക്കുന്നത്.
Time Travel ( സമയ സഞ്ചാരം )
പ്രകാശത്തിന്റെ വേഗതയ്ക്കടുത്ത് സഞ്ചരിക്കാനായാൽ...അതായത് ( 3x10^8m/s ) സെക്കന്റിൽ മൂന്നുലക്ഷം കിമി. വേഗതയിൽ സമയം നമ്മളുടെ കൈപ്പിടിയിലൊതുങ്ങും... സെക്കന്റിൽ 3 ലക്ഷം കിലോമീറ്റർ വേഗമുള്ള പ്രകാശം ഒരു വർഷത്തിൽ സഞ്ചരിക്കുന്ന ദുരമാണ് ഒരു പ്രകാശവർഷം.
പ്രകാശവർഷം = 300000 X 3600 X 24 X 365.24 കി. മി
= 9500000000000 കി. മി.
ഈ വേഗതയിൽ പ്രപഞ്ചത്തിൽ A എന്ന പോയിന്റിൽ നിന്ന് B എന്ന പോയിന്റിലേക്ക് സഞ്ചരിച്ചാൽ. തിരിച്ച് നമ്മൾ Aയിൽ എത്തുമ്പോഴേക്കും ആയിരക്കണക്കിനു വർഷങ്ങൾ കഴിഞ്ഞുപോയിരിക്കും. ചുരുക്കിപ്പറഞ്ഞാൽ നമ്മൂടെ ഏതാനും മിനിറ്റുകൾ മറ്റൊരിടത്ത് ആയിരക്കണക്കിന് വർഷങ്ങളാകും. ഒരു സഞ്ചരിക്കുന്ന വസ്തു പ്രകാശത്തിന്റെ വേഗത്തിനൊപ്പം എത്തുന്തോറും സമയം ചെറുതായി ചെറുതായി വരും. പ്രകാശത്തിന്റെ ഒപ്പം വേഗതയിൽ നമ്മൾ സമയത്തിനൊപ്പം സഞ്ചരിക്കും. ഇനി പ്രകാശവേഗത്തെ മറികടക്കാനായാൽ നമ്മൾ ചെല്ലുന്നത് ഭാവിയിലാണ്. സ്റ്റീഫൻ ഹോക്കിങ്ങ്സിന്റെ "A Breif History Of Time" എന്ന പുസ്തകത്തിൽ ആപേക്ഷികമായി പെരുമാറുന്ന സമയത്തിനെപ്പറ്റി കൂടുതൽ ലളിതമായി വിശദീകരിച്ചിട്ടുണ്ട്. അതുപോലെ "INTERSTELLAR" എന്ന ഹോളിവുഡ് ചിത്രം കണ്ടാല് നമുക്ക് എന്താണ് സമയ സഞ്ചാരം എന്ന് ഒരു ധാരണ ലഭിക്കും .
Is Time Travel Possible?
ദൂരങ്ങളെ കൈപ്പിടിയിലൊതുക്കാൻ ഐൻസ്റ്റീൻ തന്നെ ഹൈപ്പർസ്പേസിൽ ഒരു വഴി ഉണ്ട് എന്ന് പറയുകയുണ്ടായി. വേം ഹോൾ ( Worm Hole ) എന്ന തിയറി പ്രകാരം സമയത്തേയും സ്ഥലത്തെയും ബെൻഡ് ചെയ്യിച്ച് പ്രപഞ്ചത്തിന്റെ മറ്റൊരു കോണിൽ സ്മരണമാത്രയിൽ എത്താനാകും എന്നതാണത്. ഇതൊരു ഹൈപ്പോതീസിസ് ആയി നിൽക്കുകയാണിപ്പഴും. തെളിയിക്കപ്പെടാത്ത സത്യം എന്ന് വേണമെങ്കിൽ വിവക്ഷിക്കാം.X,Y,Z കൂടാതെ നാലാമത്തെ ഡയമെൻഷൻ സമയം (Time ) . അഞ്ചും ആറും ഗ്രാഫിക്കൽ എക്സ്പ്ലനേഷനുകളിലൂടെ ബോക്സ് ഇൻസൈഡ് എ ബോക്സ് എന്ന വിശദീകരണമൊക്കെ മനസ്സിലായ പോലെ ഭാവിക്കാം.
Worm Holes
സാമാന്യ ആപേക്ഷികതാസിദ്ധാന്തം ഗുരുത്വാകര്ഷണത്തെക്കുറിച്ച് തികച്ചും നൂതനമായ ഒരു കാഴ്ചപ്പാട് മുന്നോട്ടുവെച്ചു. ദ്രവ്യത്തിന്റെ സാന്നിധ്യം സമീപമുള്ള സ്ഥലത്തെ വളയ്ക്കുന്നു (മുകളിലുള്ള ചിത്രം നോകുക്ക ). ആ വക്രതയുടെ സ്വഭാവം എത്ര ദ്രവ്യം ഉണ്ട് എന്നതിനെ ആശ്രയിച്ചിരിക്കും. അങ്ങനെ ഒരു സാധ്യത ഉണ്ടെങ്കില് സ്ഥലങ്ങളെ തമ്മില് ബന്ധിപ്പിക്കുന്ന എളുപ്പമാര്ഗം അതായത് ഒരു തുരങ്കം ഉണ്ടാകാം. അതിനെയാണ് ഐന്സ്റ്റൈന് റോസെന് ബ്രിഡ്ജ് അഥവാ വോംഹോള് എന്ന് വിളിക്കുന്നത്.
ഒരു ഉദാഹരണം എടുക്കാം (മുകളിലുള്ള വീഡിയോ നോകുക്ക ) , 2 ആളുകള് ഒരു ബെഡ്ഷീറ്റ് വലിച്ചു പിടിച്ചിരിക്കുന്നു.അതിലേക്കു ഒരു ക്രിക്കറ്റ്ബാള് വെച്ചാല് എന്ത് സംഭവിക്കും? അത് ഉരുണ്ടു ബെഡ്ഷീറ്റിന്റെ മധ്യത്തിലേക്ക് ചെന്ന് അവിടെ ഒരു വക്രത സൃഷ്ടിക്കുന്നു .ഇനി ആ ഷീറ്റിന്റെ മൂലയില് ഒരു കല്ല് വെക്കുകയാണെങ്കിലോ? അത് ക്രിക്കറ്റ് ബാള് ഉണ്ടാക്കിയ വക്രത കാരണം ബാളിന്റെ് ദിശയിലേക്ക് സഞ്ചരിക്കും. ഇവിടെ നമ്മള് സ്ഥലത്തെ 2D (നീളം,വീതി) ആയിട്ടാണ് എടുത്തത്. യഥാര്ത്ഥത്തില് 4D (നീളം, വീതി, ഉയരം, സമയം) ആയിരുന്നു വേണ്ടത്. നമ്മള് ഈ ഷീറ്റിനെ മടക്കി എന്ന് കരുതുക. ഷീറ്റുകള്ക്കിടയില് സ്ഥലം വിട്ടിട്ടുണ്ട്. ഒന്നില് ഒരു ക്രിക്കറ്റ്ബാള് വെച്ചു. അവിടെ ഒരു വക്രത ഉണ്ടാകുന്നു. ഷീറ്റ് മറിച്ചുപിടിച്ച് അപ്പുറത്തെ ഷീറ്റിലും അതേ സ്ഥാനത്ത് ഒരു ബാള് വെച്ചാല് അവിടെയും ഒരു വക്രത ഉണ്ടാകുകയും അത് രണ്ടും കൂട്ടി മുട്ടുകയും ചെയ്യും. ഇതുപോലെയാണ് wormholes ഉണ്ടാകുന്നത്. പ്രപഞ്ചത്തില് സ്ഥലകാല വക്രീകരണംമൂലം രണ്ട് സ്പേസ് തമ്മില് ബന്ധിപ്പിക്കുന്ന തുരങ്കങ്ങള്(tunnels) ഉണ്ടാവാം. ഇങ്ങനെ വലിയ ദൂരങ്ങളെ ചുരുക്കി ചെറിയ ദൂരങ്ങളാക്കുന്ന പ്രതിഭാസത്തെയാണ് വോംഹോള് എന്ന് പറയുന്നത്.
രണ്ടു ബിന്ദുക്കള് തമ്മിലുള്ള ഏറ്റവും കുറഞ്ഞ ദൂരം എന്നത് അവ തമ്മിലുള്ള നേര്രേഖാ ദൂരമാണെന്ന് നാം ഹൈസ്കൂള് ക്ലാസുകളില് പഠിച്ചിട്ടുണ്ട്. എന്നാല് ആ പേപ്പര് ഒന്ന് മടക്കിയാലോ? അപ്പോള് കിട്ടുന്നതാണ് ഒരു ചതുര്മാനത്തിലെ (4Dimension) കുറഞ്ഞദൂരം. ഇത് തന്നെയാണ് വോംഹോള് മെക്കാനിസവും. എന്താണ് വോംഹോള്’ന്റെ മെച്ചം? ഉദാഹരണത്തിലൂടെ നമുക്കത് പരിശോധിക്കാം. വലിയൊരു പര്വതനിര. അതിന്റെ ഒരുവശത്തുനിന്ന് മറ്റേ വശത്തെ ബന്ധിപ്പിക്കുന്ന ഒരു തുരങ്കം നിര്മ്മിച്ചിരിക്കുന്നുവെന്ന് കരുതുക. ഒരു പര്വതാരോഹകന് പര്വതനിരകളുടെ ഒരുദിക്കില്നിന്ന് മറുദിക്കിലേക്ക് സാഹസപ്പെട്ടുനടത്തെത്താന് ഏറെ ദിവസങ്ങള് വേണ്ടിവരുമെങ്കില് തുരങ്കത്തിലൂടെ മറുദിക്കിലെത്തിച്ചേരാന് മിനിറ്റുകളോ, മണിക്കൂറുകളോ മതിയാകും. Wormholeല് സഞ്ചരിക്കാന് നമുക്ക് പ്രവൃത്തി ചെയ്യേണ്ട കാര്യമില്ല. ഗുരുത്വാകര്ഷണബലം നമ്മുടെ ത്വരണത്തെ (acceleration) വര്ധിപ്പിക്കുകയും ഗുരുത്വാകര്ഷണവലിവ് (gravitational pull) അനുഭവപ്പെടുകയും തുടര്ന്ന് വര്ധിച്ച പ്രവേഗത്തോടെ വസ്തുവിനെ മറുവശത്തേക്ക് പുറന്തള്ളുകയും ചെയ്യും. Wormhole ലൂടെയുള്ള ഈ യാത്രയില് നമ്മുടെ ക്ലോക്ക് പതുക്കെയായിരിക്കും സഞ്ചരിക്കുക. (തുടരും)

| credit: www.space.com |
2015 marks 100 years since the publication of Albert Einstein's General Theory of Relativity,
Credit: By Karl Tate, Infographics Artist








Excellent article Mr.Mohammed Shamil. Nice way of explanation and presentation. Really waiting for tis type of valuable and informative article. The saddest part about you is, you just shifted to creationism from Atheism. Hope your future post will explain why you left Atheism. Even if you disprove evolution we are always ready to hear your arguments and I really appreciate your hard work to prove creationism. The idea of extra dimension is quiet enough to prove another universe . eagerly waiting how you link all this. all the best.
ReplyDeleteWell written article - great job👍🏼
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteഇതൊക്കെ ഇത്രയും ലളിതമായും ആവിഷ്ക്കരിക്കാം അല്ലേ!!!
ReplyDelete